[ 이진 트리 ] 알고리즘

 

 

1.  개념

 

이진 트리 : 각 노드의 자식 노드의 개수가 2개 이하로 구성되어 있는 트리

 

이진 트리의 종류

-  편향 이진 트리 : 노드가 한쪽 방향으로 몰려 있는 트리

    * 탐색 속도 느림 / 공간 복잡도 큼

 

-  포화 이진 트리 : 트리의 높이가 일정하며 노드가 꽉 찬 트리

    * 포화 이진 트리의 노드의 개수 : 2^(높이+1) - 1 개

 

-  완전 이진 트리 : 노드가 순차적으로(왼 -> 오) 채워져 있는 트리

 

완전 이진 트리가 가장 자주 쓰이는 이진 트리!

 

 

2.  구현

 

이진 트리를 가장 직관적으로 표현할 수 있는 자료 구조는 '리스트'

이진 트리는 1차원 리스트로 표현한다

 

인덱스	1	2	3	4	5	6	7	8
노드	1	2	3	4	5	6	7	8

 

노드 간의 상관관계는 아래의 표에 따라 표현한다

이동 목표 노드	인덱스 연산	제약 조건 ( n : 노드 개수 )
루트 노드	index = 1
부모 노드	index = index / 2	현재 노드가 루트 노드가 아님
왼쪽 자식 노드	index = index * 2	index * 2 <= n
오른쪽 자식 노드	index = index * 2 + 1	index * 2 + 1 <= n

 

 

3.  문제

 

# 1  트리 순회하기 - 백준 1991번

https://www.acmicpc.net/problem/1991

1991번: 트리 순회

 

트리 순환

 

-  전위 순환 : 루트 -> 왼쪽 자식 -> 오른쪽 자식

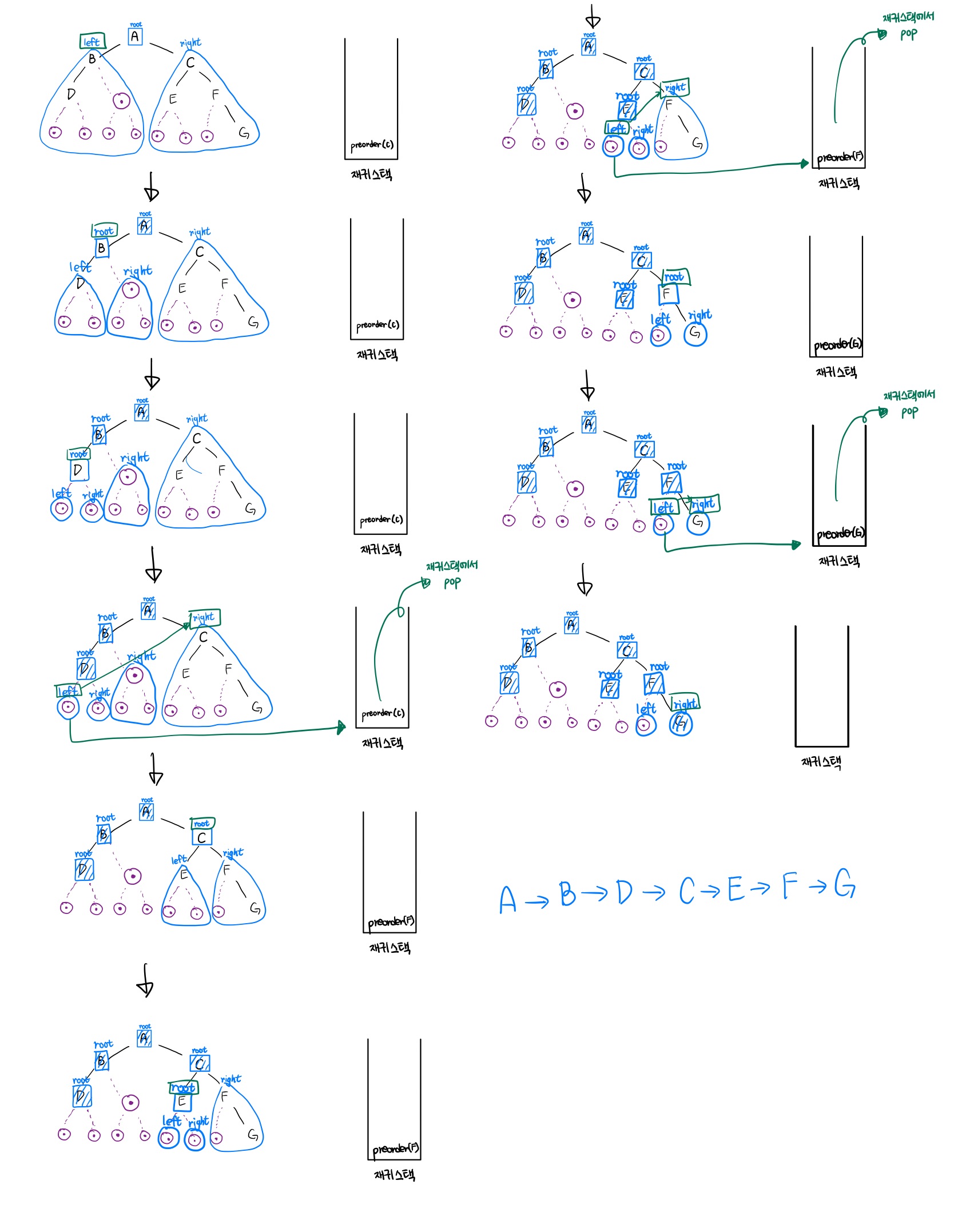
-  중위 순환 : 왼쪽 자식 -> 루트 -> 오른쪽 자식

 

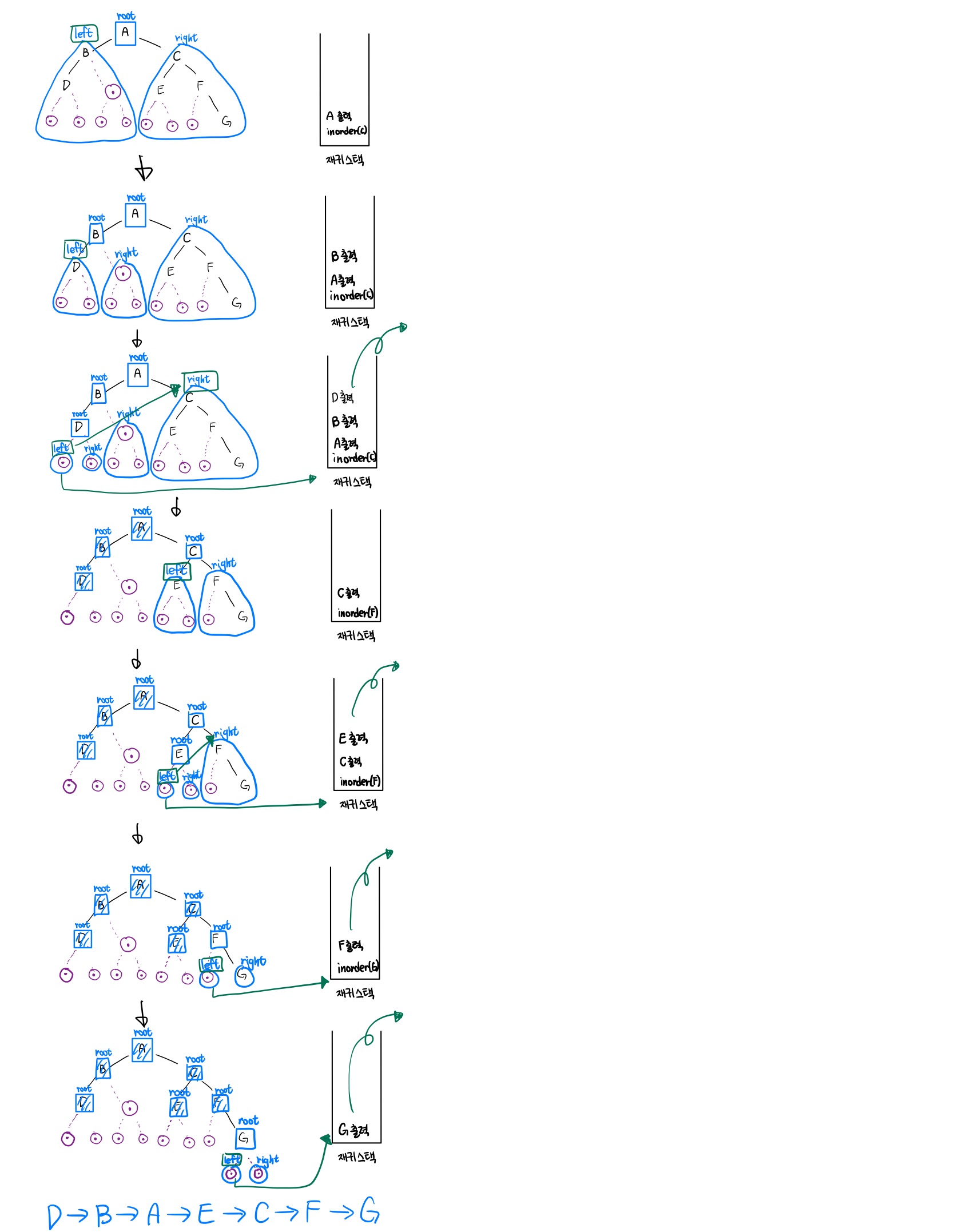
-  후위 순환 : 왼쪽 자식 -> 오른쪽 자식 -> 루트

 

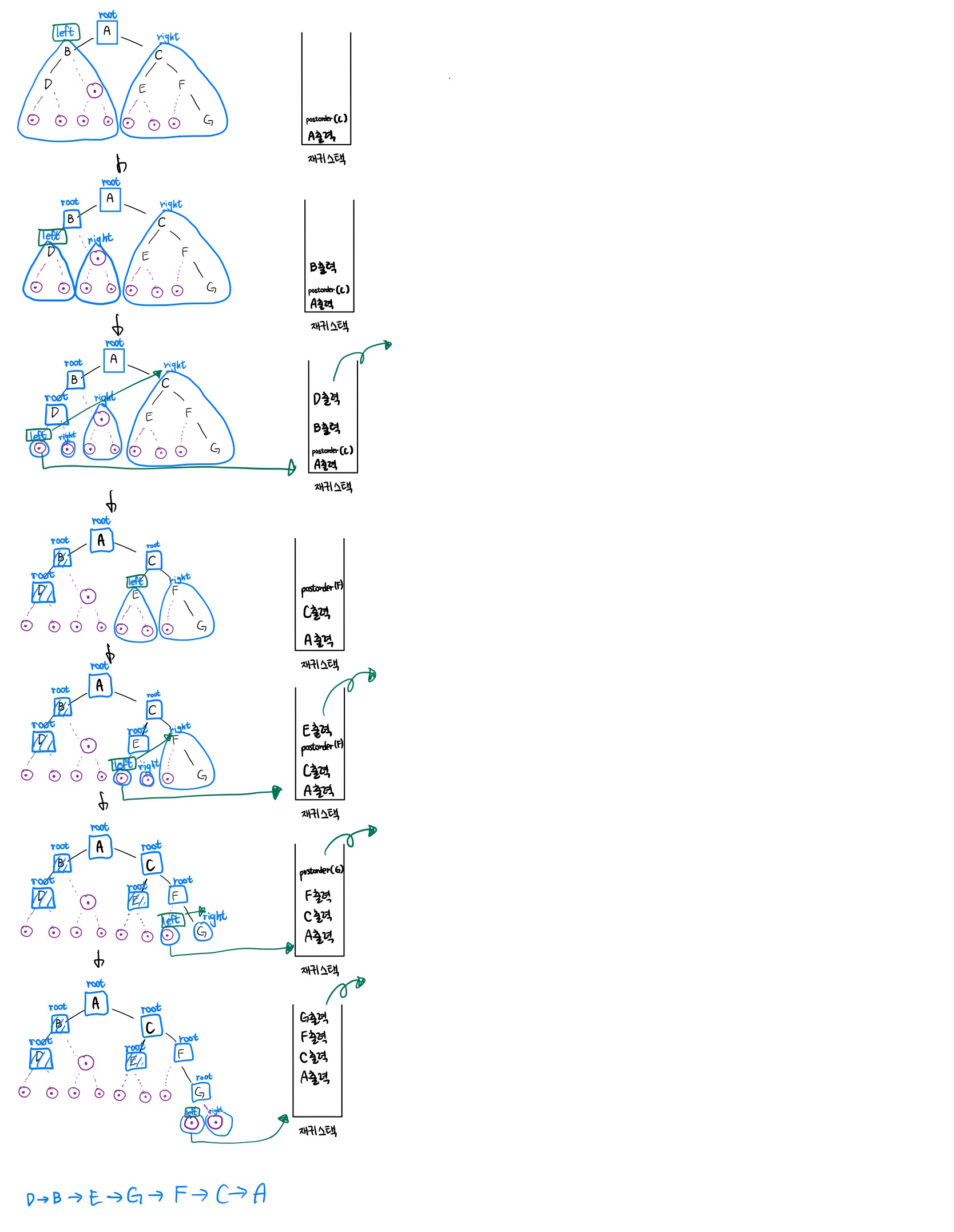
import sys
input = sys.stdin.readline

n = int(input())

# 딕셔너리로 이진 트리 구현
tree = {}
for i in range(n):
    root, left, right = map(str, input().split())
    tree[root] = [left, right]


# 전위 순환 : 루트 -> 왼쪽 자식 -> 오른쪽 자식
def preorder(v):
	# 가지의 마지막 노드 도달하면 return -> 재귀 스택에서 pop된 재귀 함수 발동
    if v == ".":
        return
    print(v, end='')	  # 루트
    preorder(tree[v][0])  # 왼쪽 자식
    preorder(tree[v][1])  # 오른쪽 자식


# 중위 순환 : 왼쪽 자식 -> 루트 -> 오른쪽 자식
def inorder(v):
	# 가지의 마지막 노드 도달하면 return -> 재귀 스택에서 pop된 재귀 함수 발동
    if v == ".":
        return
    inorder(tree[v][0])	  # 왼쪽 자식
    print(v, end='')	  # 루트
    inorder(tree[v][1])   # 오른쪽 자식


# 후위 순환 : 왼쪽 자식 -> 오른쪽 자식 -> 루트
def postorder(v):
	# 가지의 마지막 노드 도달하면 return -> 재귀 스택에서 pop된 재귀 함수 발동
    if v == '.':
        return
    postorder(tree[v][0])	# 왼쪽 자식
    postorder(tree[v][1])	# 오른쪽 자식
    print(v, end='')	    # 루트


# 루트 노드 각 함수에 삽입
preorder('A')	
print()
inorder('A')
print()
postorder('A')