[ 트리 ] 알고리즘
2023. 7. 19. 21:27ㆍ개발/👾 PS
1. 개념
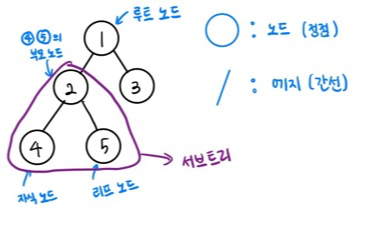
트리 : 노드(정점)와 에지(간선)로 연결된 그래프
트리는 아래의 특징을 갖는 그래프의 한 종류이다
특징
- 사이클 X
- 1개의 루트 노드가 존재
- 루트 노드를 제외한 노드는 단 1개의 부모 노드를 가짐
- 부분 트리가 존재하며 트리의 특징을 모두 따름
용어 정리
노드 : 데이터의 index와 value를 표현하는 요소 (정점)
에지 : 노드와 노드의 연결 관계를 나타내는 선 (간선)
루트 노드 : 트리에서 가장 상위에 존재하는 노드
부모 노드 : 두 노드 사이의 관계에서 상위 노드에 해당하는 노드
자식 노드 : 두 노드 사이의 관계에서 하위 노드에 해당하는 노드
리프 노드 : 트리에서 가장 하위에 해당하는 노드
서브 트리 : 전체 트리에 속한 부분 트리
2. 문제
# 1 트리의 부모 찾기 - 백준 11725번
https://www.acmicpc.net/problem/11725
11725번: 트리의 부모 찾기
루트 없는 트리가 주어진다. 이때, 트리의 루트를 1이라고 정했을 때, 각 노드의 부모를 구하는 프로그램을 작성하시오.
www.acmicpc.net

import sys
input = sys.stdin.readline
n = int(input())
node = [[] for _ in range(n+1)] # 인접리스트
stack = []
visited = [False for _ in range(n+1)]
parent = [-1 for _ in range(n+1)] # 부모 노드 리스트
# 인접 리스트 생성
for i in range(n-1):
u, v = map(int, input().split())
node[u].append(v)
node[v].append(u)
node[u].sort()
node[v].sort()
# dfs
def dfs(a):
while stack:
v = stack.pop()
for i in node[v]:
if not visited[i]:
visited[i] = True
parent[i] = v # 부모 노드 저장하기
stack.append(i)
stack.append(1)
dfs(1)
for i in range(2, n+1):
print(parent[i])
# 2 리프 노드의 개수 구하기
https://www.acmicpc.net/problem/1068
1068번: 트리
첫째 줄에 트리의 노드의 개수 N이 주어진다. N은 50보다 작거나 같은 자연수이다. 둘째 줄에는 0번 노드부터 N-1번 노드까지, 각 노드의 부모가 주어진다. 만약 부모가 없다면 (루트) -1이 주어진다
www.acmicpc.net


n = int(input())
parent = list(map(int, input().split()))
delNode = int(input())
visited = [False for _ in range(n)]
start = -1
result = 0
node = [[] for _ in range(n)]
for i in range(n):
if parent[i] == -1: # 시작 노드 설정
start = i
else: # 인접 리스트 초기화
node[i].append(parent[i])
node[parent[i]].append(i)
#dfs
def dfs(v):
cNode = 0 # 자식 노드 수
global result
visited[v] = True
for i in node[v]:
if not visited[i] and i != delNode: # 삭제 노드면 탐색 중지
cNode += 1
dfs(i)
# 자식 노드 수가 0이면 result 1 증가
if cNode == 0:
result += 1
if delNode == start:
print(0)
else:
dfs(start)
print(result)
'개발 > 👾 PS' 카테고리의 다른 글
| [ 이진 트리 ] 알고리즘 (0) | 2023.07.26 |
|---|---|
| [ 트라이 ] 알고리즘 (0) | 2023.07.22 |
| [ 최소 신장 트리 ] 알고리즘 (0) | 2023.07.19 |
| [ 플로이드 - 워셜 ] 알고리즘 (0) | 2023.07.18 |
| [ 벨만 - 포드 ] 알고리즘 (0) | 2023.07.15 |