2023. 8. 23. 00:31ㆍ개발/👾 PS
1. 개념
세그먼트 트리 : 주어진 데이터를 이진 트리에 삽입한 후 목적에 맞게 트리를 초기화한 자료구조
세그먼트 트리 활용 : 1 ) 구간 합 2 ) 최솟값, 최댓값 구하기
세그먼트 트리를 이용할 때 데이터 업데이트가 필요한 경우 이를 빠르게 수행할 수 있다는 장점이 있다.
2. 구현
1 ) 트리 초기화
세그먼트 트리는 이진 트리를 이용해 구현한다.
* 파이썬에서 이진 트리는 리스트로 구현한다.
( 1 ) 트리의 크기
주어진 데이터뿐만 아니라 질의값(구간 합, 최댓값 / 최솟값)에 대한 데이터 또한 포함해야 하기 때문에
세그먼트 트리의 크기는 데이터의 개수(N)보다 넉넉하게 커야 한다.
2ᵏ >= N 을 만족하는 k의 최솟값에 대해 ( 2ᵏ * 2 ) 가 트리의 크기가 된다.
예를 들어 N(데이터의 개수) = 9일 경우 2⁴ >= 9이므로 k = 4이고 세그먼트 트리의 크기는 2⁴ * 2 = 32
( 2 ) 트리에 데이터 삽입하기
우선 주어진 데이터를 먼저 리프 노드에 삽입한다.
세그먼트 트리에서 리프 노드의 시작 인덱스는 2ᵏ 다.
세그먼트 트리(A)의 빈 부분은 목적( 구간 합, 최솟값 / 최댓값 )에 따라 채워주면 된다.
자식 노드( 2n, 2n + 1 )를 기준으로 부모 노드( n )를 채워가는 방식으로 구현한다.
- 구간 합 -> A[n] = A[2n] + A[2n+1]
- 최댓값 -> A[n] = max( A[2n], A[2n+1] )
- 최솟값 -> A[n] = min( A[2n], A[2n+1] )
2 ) 질의값 구하기
( 1 ) 질의 인덱스 => 세그먼트 트리 인덱스
세그먼트 트리 index = 질의 index + 2ᵏ - 1
주어진 데이터는 세그먼트 트리의 리프 노드( 시작점 : 2ᵏ )에 삽입되기 때문이다.
( 2 ) 현재 노드의 선택 여부 결정
현재 노드를 선택한다는 것은 현재 노드가 최종 결과값(질의값)에 영향을 주도록 한다는 것이다.
선택 여부에 따라 부모 노드로 이동하거나 부모 노드를 대상 범위에서 제거해가면서 값을 구한다.
현재 노드가 아래와 같은 조건을 만족할 때 현재 노드를 선택해준다.
* start_index % 2 == 1 (홀수) -> 시작 노드에서 출발한 노드
* end_index % 2 == 0 (짝수) -> 마지막 노드에서 출발한 노드
세그먼트 트리는 이진 트리를 이용해 구현되었기 때문에
부모 노드(n)의 왼쪽 자식(2n)의 인덱스는 짝수이며 오른쪽 자식(2n+1)의 인덱스는 홀수다.
따라서 시작 노드 혹은 시작 노드에서 출발한 노드의 인덱스가 홀수일 경우(오른쪽 자식일 경우)
해당 노드의 부모 노드는 왼쪽 자식도 포함하기 때문에 질의 인덱스 범위를 넘어가게 된다.
마찬가지로 마지막 노드 혹은 마지막 노드에서 출발한 노드의 인덱스가 짝수일 경우(왼쪽 자식일 경우)
해당 노드의 부모 노드는 오른쪽 자식도 포함하기 때문에 질의 인덱스 범위를 넘어가게 된다.
현재 노드의 부모 노드가 질의 인덱스 범위를 넘어가게 되는 경우
현재 노드를 선택해주어 현재 노드가 최종값에 직접 영향을 주도록 하는 것이다.
반대로 현재 노드의 부모 노드가 질의 인덱스 안에 포함된다면
현재 노드를 선택하지 않은 채로 부모 노드로 이동해준다.
( 3 ) 최종 결괏값 구하기
* 구간 합 : 선택된 노드들의 합 출력
* 최댓값 : 선택된 노드들 중 MAX값 출력
* 최솟값 : 선택된 노드들 중 MIN값 출력
3 ) 데이터 업데이트하기
* 구간 합 : 원래 데이터와 변경 데이터의 차이만큼 부모 노드로 올라가면서 변경
* 최댓값 : 변경 데이터와 자신과 같은 부모를 지니고 있는 다른 자식 노드와 비교 -> 더 큰 값
* 최솟값 : 변경 데이터와 자신과 같은 부모를 지니고 있는 다른 자식 노드와 비교 -> 더 작은 값
3. 문제
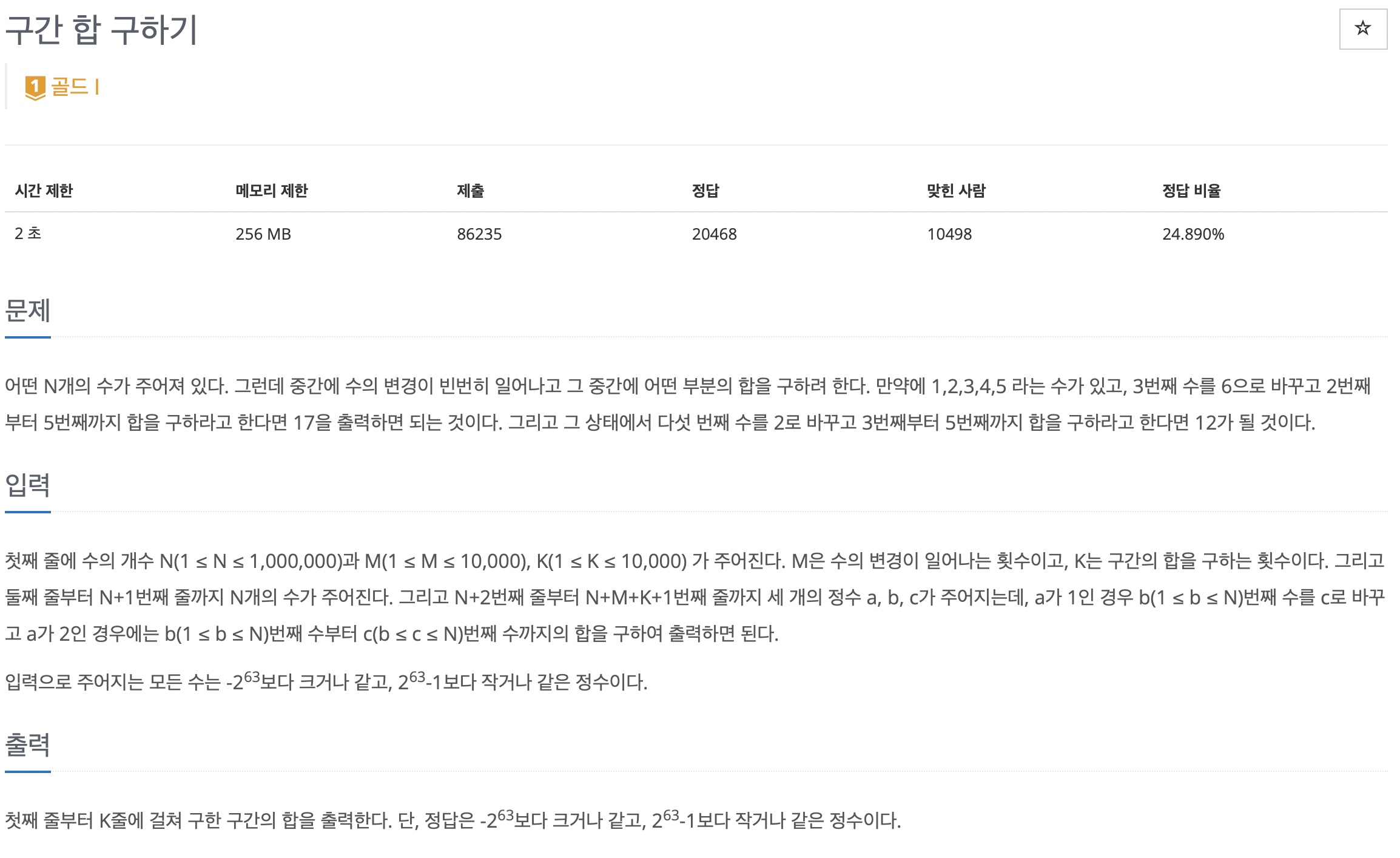
# 1 구간 합 구하기 3 - 백준 2042번
https://www.acmicpc.net/problem/2042
2042번: 구간 합 구하기
첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000,000)과 M(1 ≤ M ≤ 10,000), K(1 ≤ K ≤ 10,000) 가 주어진다. M은 수의 변경이 일어나는 횟수이고, K는 구간의 합을 구하는 횟수이다. 그리고 둘째 줄부터 N+1번째 줄
www.acmicpc.net
import sys
input = sys.stdin.readline
n, m, k = map(int, input().split())
length = n
size = 0
# 트리 크기 구하기
while length != 0:
length //= 2
size += 1
size = pow(2, size+1)
tree = [0] * (size+1)
# 주어진 데이터를 알맞은 트리 인덱스에 삽입
leftNodeStartIndex = size // 2 - 1
for i in range(leftNodeStartIndex + 1, leftNodeStartIndex + n + 1):
tree[i] = int(input())
# 트리 생성
def setTree(i):
while i != 1:
tree[i//2] += tree[i]
i -= 1
setTree(size-1)
# 데이터 업데이트
def changeVal(index, value):
# 원래 데이터와 변경 데이터의 차이를 부모 노드에 더해주기
diff = value - tree[index]
while index > 0:
tree[index] = tree[index] + diff
index = index // 2
# 질의값(구간 합) 구하기
def getSum(s, e):
partSum = 0
while s <= e:
# 특정 조건 만족하면 노드 선택해주기(구간 합에 바로 더해주기)
if s % 2 == 1:
partSum += tree[s]
s += 1
if e % 2 == 0:
partSum += tree[e]
e -= 1
# 부모 노드로 이동
s = s // 2
e = e // 2
return partSum
for _ in range(m+k):
question, s, e = map(int, input().split())
if question == 1:
changeVal(leftNodeStartIndex + s, e)
elif question == 2:
s += leftNodeStartIndex
e += leftNodeStartIndex
print(getSum(s, e))
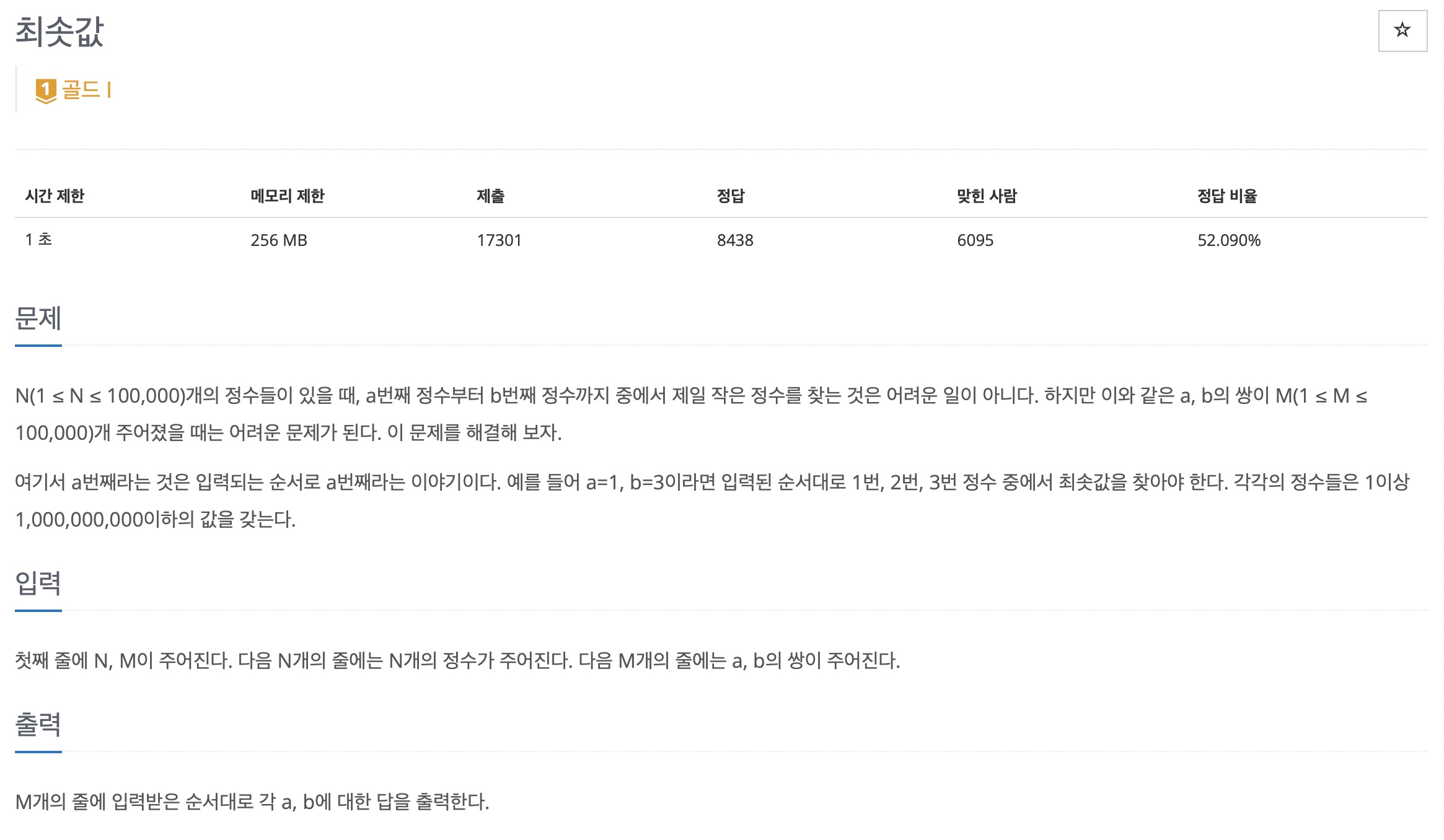
# 2 최솟값 찾기2 - 백준 10868번
https://www.acmicpc.net/problem/10868
10868번: 최솟값
N(1 ≤ N ≤ 100,000)개의 정수들이 있을 때, a번째 정수부터 b번째 정수까지 중에서 제일 작은 정수를 찾는 것은 어려운 일이 아니다. 하지만 이와 같은 a, b의 쌍이 M(1 ≤ M ≤ 100,000)개 주어졌을 때는
www.acmicpc.net
import sys
input = sys.stdin.readline
n, m = map(int, input().split())
length = n
size = 0
while length != 0:
length //= 2
size += 1
size = pow(2, size+1)
tree = [10**10] * (size+1)
leftNodeStartIndex = size // 2 - 1
for i in range(leftNodeStartIndex + 1, leftNodeStartIndex + n + 1):
tree[i] = int(input())
# 트리 생성하기 -> 부모 노드에 자식 노드 둘 중 더 작은 노드로 저장하기
def setTree(i):
while i != 1:
tree[i//2] = min(tree[i], tree[i//2])
i -= 1
setTree(size-1)
# 질의값 구하기
## 특정 조건 만족하면 노드 numList에 저장하기 / 부모 노드 배제
## 조건 만족하지 않으면 부모 노드로 이동
def getMin(s, e):
numList = []
while s <= e:
if s % 2 == 1:
numList.append(tree[s])
s += 1 # 부모 노드 배제
if e % 2 == 0:
numList.append(tree[e])
e -= 1 # 부모 노드 배제
# 부모 노드로 이동
s = s // 2
e = e // 2
return min(numList)
for i in range(m):
a, b = map(int, input().split())
print(getMin(a+leftNodeStartIndex, b+leftNodeStartIndex))
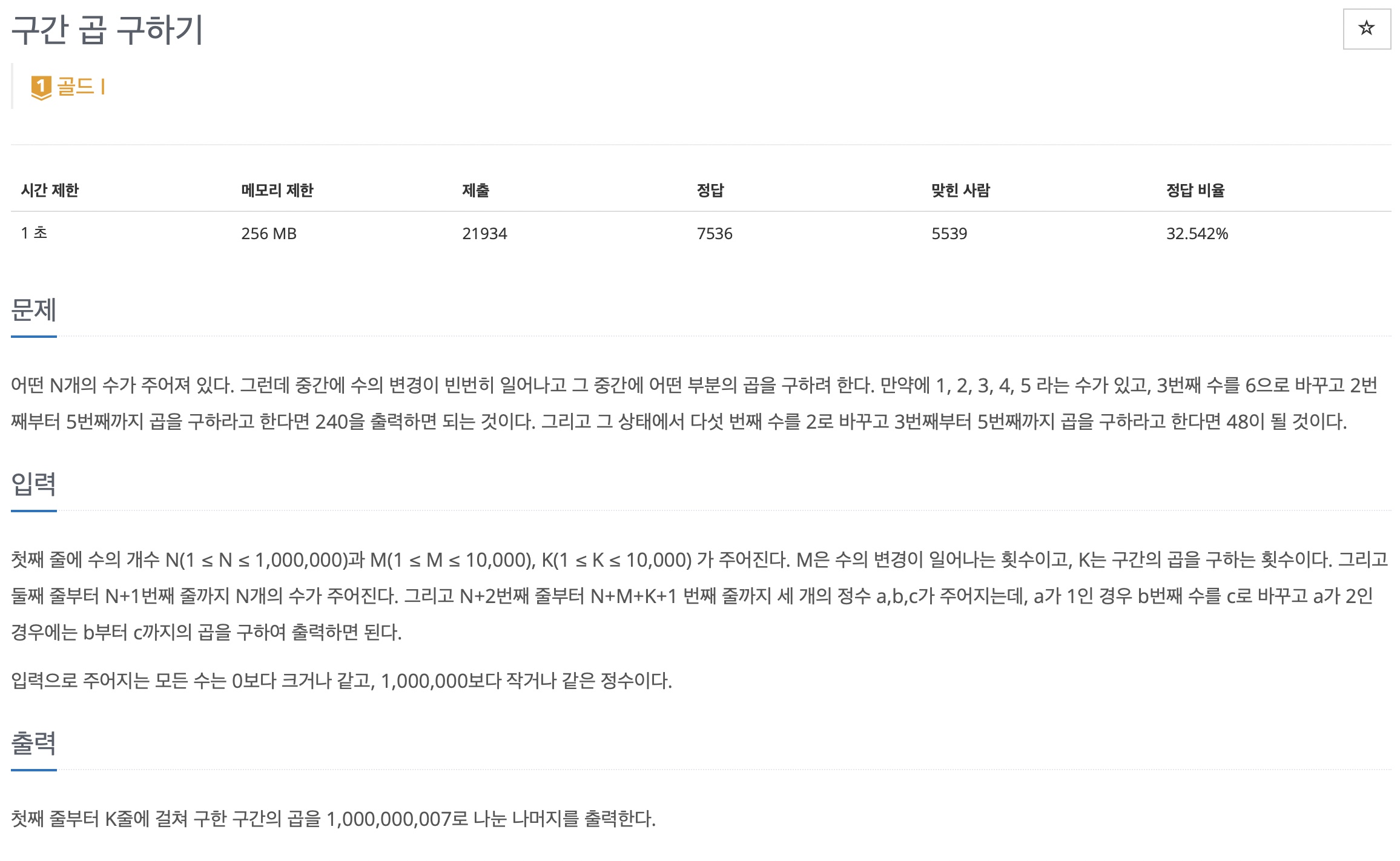
# 3 구간 곱 구하기 - 백준 11505번
https://www.acmicpc.net/problem/11505
11505번: 구간 곱 구하기
첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000,000)과 M(1 ≤ M ≤ 10,000), K(1 ≤ K ≤ 10,000) 가 주어진다. M은 수의 변경이 일어나는 횟수이고, K는 구간의 곱을 구하는 횟수이다. 그리고 둘째 줄부터 N+1번째 줄
www.acmicpc.net
import sys
input = sys.stdin.readline
n, m, k = map(int, input().split())
length = n
size = 0
# 트리 크기 구하기
while length != 0:
length //= 2
size += 1
size = pow(2, size+1)
tree = [1] * (size+1)
# 주어진 데이터를 알맞은 트리 인덱스에 삽입
leftNodeStartIndex = size // 2 - 1
for i in range(leftNodeStartIndex + 1, leftNodeStartIndex + n + 1):
tree[i] = int(input())
# 트리 생성
def setTree(i):
while i != 1:
tree[i//2] *= tree[i]
i -= 1
setTree(size-1)
# 데이터 업데이트
def changeVal(index, value):
if tree[index] == 0:
for i in range(leftNodeStartIndex+1):
tree[i] = 1
tree[index] = value
setTree(size-1)
else:
diff = value / tree[index]
while index > 0:
tree[index] = tree[index] * diff
index = index // 2
# 질의값(구간 곱) 구하기
def getProduct(s, e):
partProduct = 1
while s <= e:
# 특정 조건 만족하면 노드 선택해주기(구간 곱에 바로 곱해주기)
if s % 2 == 1:
partProduct *= tree[s]
s += 1
if e % 2 == 0:
partProduct *= tree[e]
e -= 1
# 부모 노드로 이동
s = s // 2
e = e // 2
return partProduct
for _ in range(m+k):
question, s, e = map(int, input().split())
if question == 1:
changeVal(leftNodeStartIndex + s, e)
elif question == 2:
s += leftNodeStartIndex
e += leftNodeStartIndex
print(int(getProduct(s, e) % 1000000007))
으엥 오버플로우 에러 난당...ㅠ
검색해보니까 모듈러 계산해야 하는 듯....
일단 다음에...!
'개발 > 👾 PS' 카테고리의 다른 글
| 🍉 2023 SUAPC SUMMER 🍉 (0) | 2023.09.11 |
|---|---|
| [ 최소 공통 조상 ] 알고리즘 (1) | 2023.08.23 |
| 📣 솔브드 그랜드 아레나 📣 (0) | 2023.08.16 |
| [ 이진 트리 ] 알고리즘 (0) | 2023.07.26 |
| [ 트라이 ] 알고리즘 (0) | 2023.07.22 |